Welcome back!
Last week I mentioned that the next step would be to work on translating Kernal.gs and Driver.gs. These files contain many important functions for the entire game engine, including the main game loop and the initialization before it. These two files are distinct in the context of the apple IIGS, but for our purposes many functions in Driver are not needed (hardware specific interaction that is handled differently by ScummVM such as user input), and the remaining ones are not distinct enough from Kernal to require their own file. The functions from both of them are core to the engine in general, so they will all be methods of the main engine class anyway.
I have been wanting to discuss my process and methodology for translating the engine structure, but I haven’t found quite the right way to phrase it just yet, so I will leave that to another time.
For this post, I would instead like us to move our scope from the engine as a whole, all the way down to the individual bits and bytes for a moment.
I think we have some interesting things to nyble on for a little bit. Don’t worry though! I didn’t byte off more than I can chew. Compared to last week, this will be much less wordy. So hopefully you won’t find yourself scrolling at double time because it’s getting too long.
Alright I think got all the puns out of my system, lets get into it.
What’s in a palette?
The example we will use for this, will be all about processing the palette. The Immortal uses the Apple IIGS High-res mode at 320×200, which allows for 4bpp (bits per pixel) colour depth. What this means, is that every pixel on the screen gets a total of 4 bits to express the colour it will display. With 4 bits only having up to 0xF (15), it can pick from a palette of 16 total colours. The Apple IIGS was capable of displaying 4096 unique colours, (0xFFF) in hex. This means that each of the unique colours can be described with 12 bits, 0x000-0xFFF. However the smallest container of memory available to work with is a byte, which is 8 bits. So to store a single colour, you need 2 bytes. This means that a palette gets stored in memory as a sequence of 16 words, and each pixel is a 4 bit reference to the index of one entry.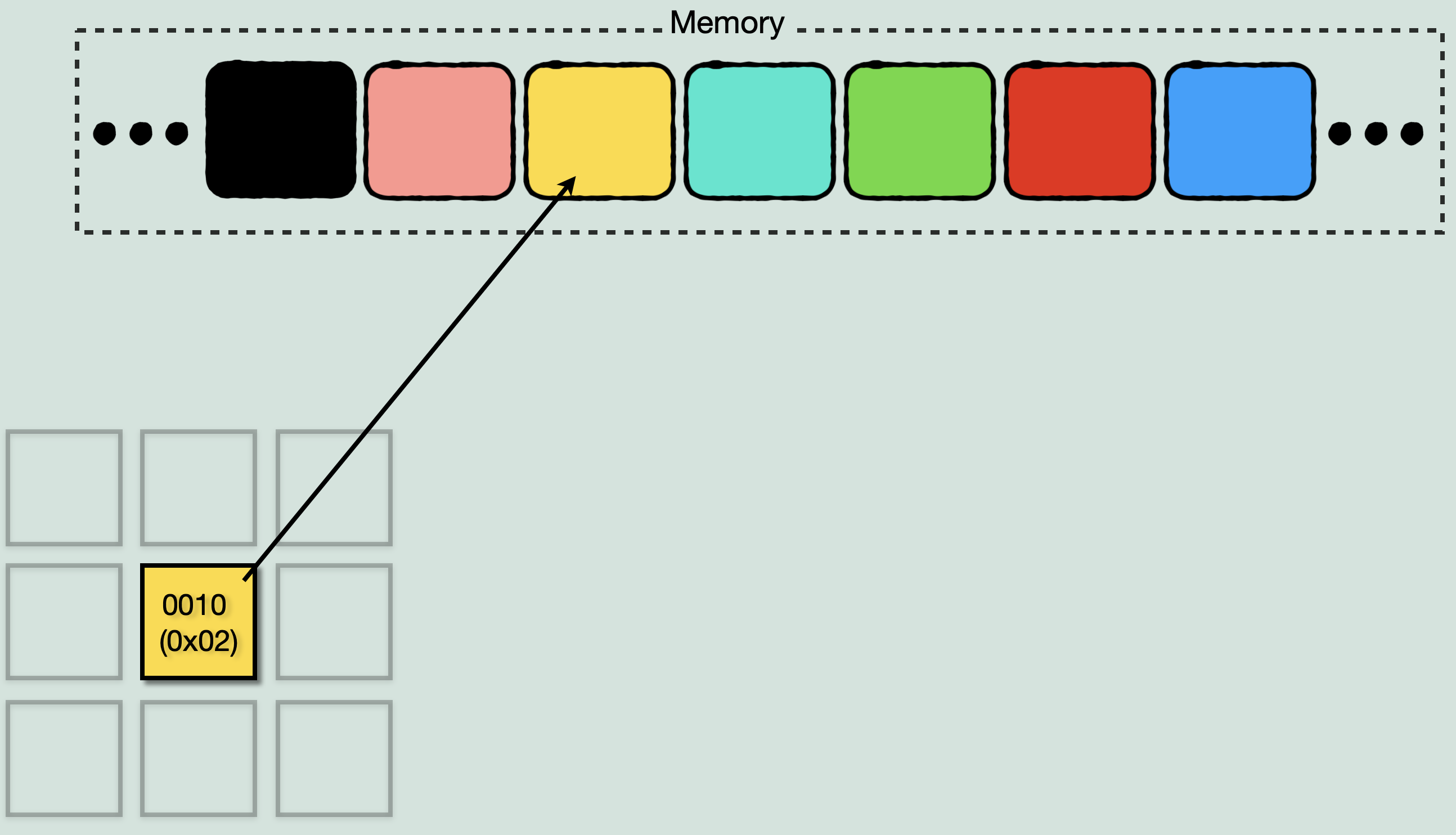
We will come back to this in a second. First, how does ScummVM handle palette data compared to the Apple IIGS? We’ll talk more about what an image actually is in a later post, but the important part for this post is that ScummVM has the ability to simulate the colour memory of computers from this time. This is represented as an array of up to 256 entries, where every entry is 3 bytes representing the Red, Green, and Blue intensity (brightness) of a given palette entry, with the final byte of the palette being used for transparency. This allows for 16 palettes of 16 colours each. For the Apple IIGS however, we only need a single palette. ScummVM is able to apply this palette to a ‘surface’, which presents the game screen. This means that to take the palette from the game, and apply it to the ScummVM surface, we need to extract those 4 bit colour values and turn them into RGB bytes for the surface.
This is a good example of simple bit manipulation because it only requires that we separate the parts of the word, and make it fit the size of the RGB data. So let’s take a quick look at that:
void ImmortalEngine::setColors(uint16 pal[]) {
// The RGB palette is 3 bytes per entry, and each byte is a colour
for (int i = 0; i < 16; i++) {
// Check for negative
if (pal[i] < kMaskNeg) {
_palRGB[(i * 3)] = ((pal[i] & kMaskRed) >> 4);
_palRGB[(i * 3) + 1] = ((pal[i] & kMaskGreen));
_palRGB[(i * 3) + 2] = (pal[i] & kMaskBlue) << 4;
}
}
// Palette index to update first is 0, and there are 16 colours to update
g_system->getPaletteManager()->setPalette(_palRGB, 0, 16);
g_system->updateScreen();
}
This function takes in a palette pal which is an array of 16 uint16 (2 unsigned bytes), and loops over it. It does a check for the value being a negative (in the context of 65816, the negative status flag is triggered on values 0x8000-0xFFFF) so that this routine can update specific colours alone by masking the other entries with 0xFFFF values. If we have a palette value that is supposed to be used to update the current surface palette, we break it up into its component colours. To do this, we will need to use the & (AND) operator to mask only the 4 bits that represent each colour, and assign those bits separately to each byte of the RGB palette. So, remembering the position of each colour as a nyble in the word, we could say for example: byte RED = pal[i] & 0x0F00;
However, masking the bits doesn’t change their position, it just isolates them. Because the red bits are in the first nyble of the second byte, the value we get returned is still 2 bytes long, which is bigger than the single byte we want to assign it to. To change the position of bits within a value, we can use another bitwise operator, >> (LSR). This operator will ‘shift’ all the bits in a value to the right a specific number of times, discarding the bits whose position is being moved into by the bits next to them. This is more or less equivalent to dividing the number by 2 each time. Now we can just count the number of bits required to move it into position. So for red, to get it to the end of the value so that it can be used as a single byte, we can say: byte RED = (pal[i] & 0x0F00) >> 8;
One more thing needs to be kept in mind though, and that is the fact that the RGB bytes used by ScummVM have a much larger range of intensity. They can use 8 bits, so they can be any brightness from 0 to 255, where as the colour value represented by the palette used by The Immortal only has 4 bits, and therefor only ranges from 0 to 15. So we need to multiply the native colour value by 4 extra bits to get the proportionate RGB value. To do this we can say: byte RED = ((pal[i] & 0x0F00) >> 8) << 4;
At this point we can see the statement can be simplified. The position of the red bits is 8 bits away from it’s native value in the new byte, but it’s only 4 bits away from the larger value we need to turn it into anyway. So finally we can combine them and instead say: _palRGB[(i * 3)] = ((pal[i] & kMaskRed) >> 4);
This is all well and good for extracting colour values to simply store them somewhere else. But what about when we need to extract the colour values, do something to them, and then put them back? Well this is something games have to do frequently, and if there is something assembly language is exceedingly good at, it’s bitwise operations. So let’s take an example of a function from the game that has to extract, manipulate, and put back colour values in the palette, the colour fade routine.
Colour Fade
The routine has quite a few operations, so for the sake of clarity, and not directly transcribing the source, I have written just the important operations and filled in where context was removed:
Alright, let’s analyze this code snippet:
The purpose of this loop is to fade each colour within each entry in the palette, and store them to an output palette which used by the hardware. It achieves this the same way regardless of direction. The part I want to highlight is the bit manipulation, so to save some time I’ll explain the over arching logic for how it does this.
The colours need to fade to or from black, with the other point being whatever the original colour value was. So if the original colour was 2, and it is fading to black, it only needs to step down by 2. But if another colour is 14, then it needs to step down by a factor 7 times larger than the first colour. And for a fade to look good, it should feel like the image as a whole is getting darker at the same rate. Otherwise the colour with value 2 will be gone instantly but the really bright colours will be there for much longer, making the imagine darken in an uneven way. To put it another way, the brightness should change, but not the contrast between colours. However, if every colour gets darker by 10% of their original value, then the contrast between colours doesn’t change. The values will move up or down proportionally, and each colour will get to zero at roughly the same time.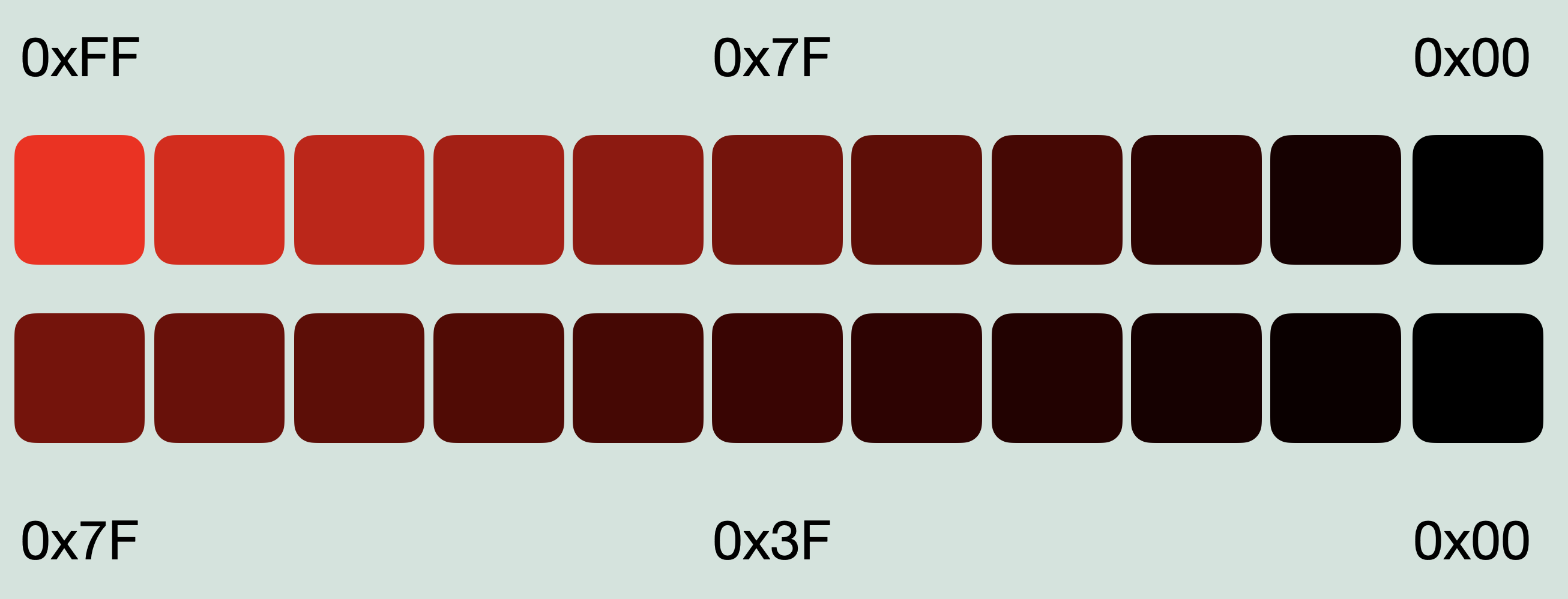
But, we don’t have hardware based division on the 65816 outside of LSR. So how do we get a percentage? We multiply by the percentage and then simply disregard the bytes beyond the whole number. Okay, let’s see what it does to these numbers:
We can start by grouping the operations by the overall purpose. We can see lda [PAL],y at three different points. These will be start for each group of operations. We need to extra three colours, and we load the original value three times. Let’s take a look at the first group, and list out the logic:
Remembering that MULTIPLIER being loaded into X just prepares the MULTIPLY routine with a multiplicand, we can write this as:
From the palette entry, take just the nyble containing the blue value -> multiply the blue value by the percentage out of 0x100 (256) -> flip the byte order of the result and take just the last nyble -> store to the blue portion of the final value.
The first part is pretty simple, we take the blue and multiply it up. The next bit is where it gets interesting. XBA will flip the byte order (as discussed in a previous post), making XXYY -> YYXX. This can be used in all kinds of ways, but here we get to see it used to perform a clever shortcut for division. After the multiplication, we have B*percent of 0x100. So from 000B we get 0BBB. But we only want 0B00, we only want 4 bits of precision, not 12. We can remove the extra bits by masking, but we still need to get B into a form we can use, that being 4 bits. Normally we would LSR 8 times, but XBA lets us do the sort of thing you don’t get to do much in a higher level (for good reason), it lets us use a fundamentally different mechanic to get the same result. It can’t be overstated how much of a difference this kind of thing can be. We can look at the number of cycles per operation and compare (3 + 2 = 5 vs 2 * 8 = 16), but it doesn’t really illustrate the point, because it’s not just about being more efficient with the same tool, it’s more like one way is a pencil, and the other is a pair of scissors.
From the palette entry, shift over by one nyble and grab just that -> multiply by percentage -> grab the whole number like before -> shift into position that green needs to be for the final value, and then apply those bits to the in-progress final value. And finally, we have one that uses all those things together to get the green portion:
For the sake of preserving the specific bit logic of the original, I’ve added a function for now that performs the same operation as XBA. This allows the logic to look very similar in C, and makes sure any inaccuracies from tricks like that get preserved. I will likely remove it later on and simplify logic for this kind of thing once everything is translated accurately initially.
*mult16() is just so I don’t have (uint16) everywhere, the multiplication itself is the same*
// Blue = 0RGB -> 000B -> 0BBB -> BB0B -> 000B
result = (xba(mult16((result & kMaskFirst), count))) & kMaskFirst;
// Green = 0RGB -> 00RG -> 000G -> 0GGG -> GG0G -> 000G -> 00G0 -> 00GB
temp = mult16(((pal[i] >> 4) & kMaskFirst), count);
temp = (xba(temp) & kMaskFirst) << 4;
result = temp | result;
// Red = 0RGB -> GB0R -> 000R -> 0RRR -> RR0R -> 000R -> 0R00 -> 0RGB
temp = xba(pal[i]) & kMaskFirst;
temp = xba(mult16(temp, count));
temp = xba(temp & kMaskFirst);
result = temp | result;
And after examining the palette fade at the microscopic level, let’s watch it in action at the macroscopic level:

Next week, more on the structure of the engine and how the translation for different files and functions is going.
Until then, I think I’ll take my puns and wax poetic for a bit (or maybe a byte):
One bit, Two bit, Red bit, Blue bit,
Green bit, Blue bit, Test if True bit,
This word has a little endian.
My post won’t seem to end-again.
Say! What a lot of wiseBit puns there are. (might need to XBA that middle word!)
Yes. Some bits are False, and some are True.
Some I’m told, are complimentary too.
Some are high and some are low,
And some so high they’re in an or-bit (on second thought, it’s not exclusive)
What if I roll, left shift then add?
Nope! it doesn’t work because I’m bad.

Mind that shift as multiply to rescale the color components. It will pad the value as opposed to fill in the bits correctly. Colors will look rather lackluster if you don’t fill the bits correctly. The formally correct way is to translate to a normalized float and then translate to the new unit. But you will get “good enough” results just by repeating the bits that you do have.
That is indeed something we discussed yesterday and that will be fixed.
For the sake of precision, in the case where we convert a nybble to a byte, repeating the bits is not just “good enough” but is equivalent to performing the arithmetic conversion:
C / 15 * 255 = C * (255 / 15) = C * 17 = C * 16 + C = (C << 4) | C