Tobia Tesan codes like a cow – my GSoC blog with ScummVM

In many of the more relaxed civilizations on the Outer Eastern Rim of the Galaxy, the Hitchhiker’s Guide has already supplanted the great Encyclopaedia Galactica as the standard repository of all knowledge and wisdom, for though it has many omissions and contains much that is apocryphal, or at least wildly inaccurate, it scores over the older, more pedestrian work in two important respects. First, it is slightly cheaper; and second, it has the words “DON’T PANIC” inscribed in large friendly letters on its cover.

—Hitchhiker’s Guide to the Galaxy

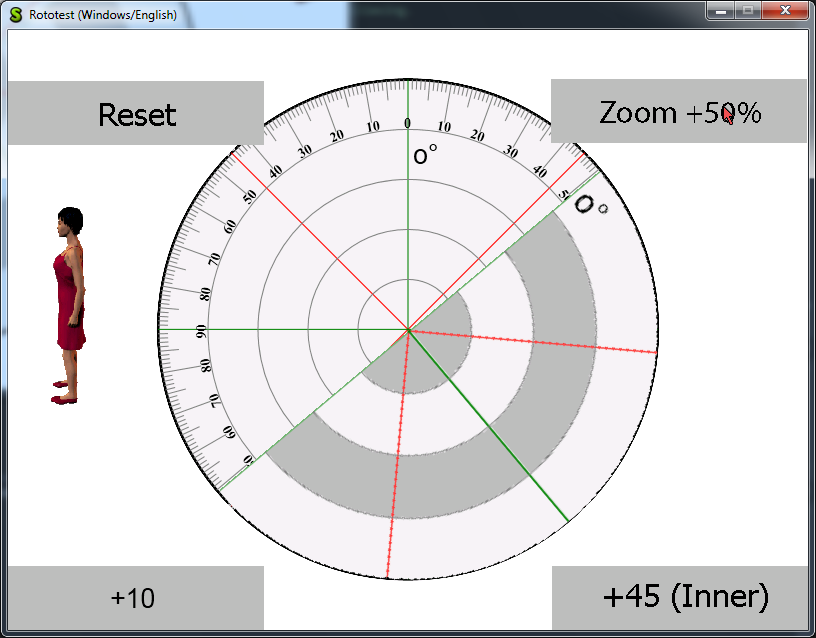
This is post will go into some detail explaining how to actually rotate a sprite in practice.
It’s a good starting point if you are rolling your own rotozoom function.
It has, naturally, zero academic value and I am also quite sure you can buy manuals that will give you a better idea for just a few dollars.
And you can always troll IRC.
But still.

Now, we assume a little knowledge of linear algebra.
You can probably go ahead all the same if you haven’t taken Algebra 101, but it makes much more sense if you have.
There is countless algebra books which will teach you the basics. Try Strang’s or Nicholson’s.

That said.
Let’s dive in.
Well, a sprite is a matrix of pixels, all right?
To rotate, zoom it and do all the nice things we want to do we need to match a pixel in the source matrix to a pixel in the destination matrix and copy its color.
“This goes here”.

So – look at the source pixel, calculate where it ends up and copy that color. [well, almost, hold on].

Copying a byte is something very simple and your language of choice already offers support for that.
Calculating the destination, well, we need a function for that.
So we have:

(x’, y’) = f(x, y, phi)

don’t we?
There is the textbook formula for rotation:

I’m not giving you a proof or anything (hey, if books aren’t enough you can easily trick a doctoral student into doing the job for you)- it just works.
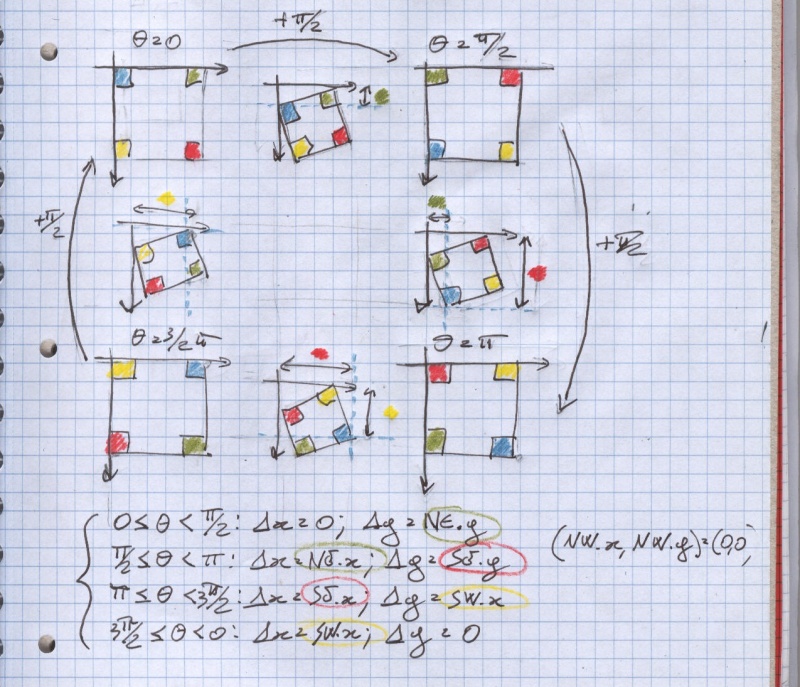
We assume that rotation is carried out around the origin and that no zooming is involved.

Zooming is actually rather trivial (just multiply by the desidred amount), rotating around a custom point basically means shifting the whole thing so that the hotspot is the new origin, then rotating as above, then shifting again so that the hotspot is where it was in the first place and everything else has moved.
Once you’ve got the simple case, it’s rather simple, though.
See also:

That’s it. Now we can match a point in our destination sprite to a point in our source sprite.
Well, this is not quite it.
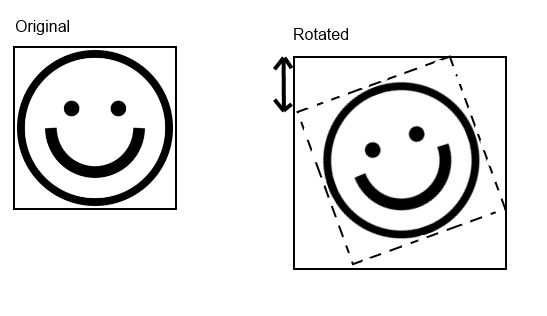
You see, while rotating points is a rather mundane matter, we are dealing with pixels, that is… we are working in the discrete.
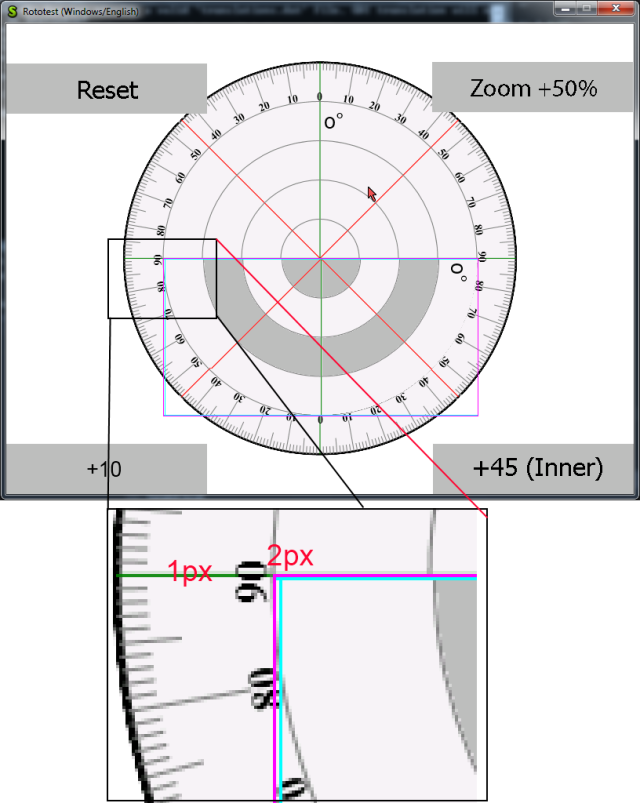
As you can see in the drawing below, P (x,y) in the destination sprite does not match exactly any pixel in the source.

Which means that we must do some approximation.
What do we do? Well, we can either round to the nearest integer or interpolate.
Interpolation will be the subject of the next post, for the moment, we round.
We basically want something like a).

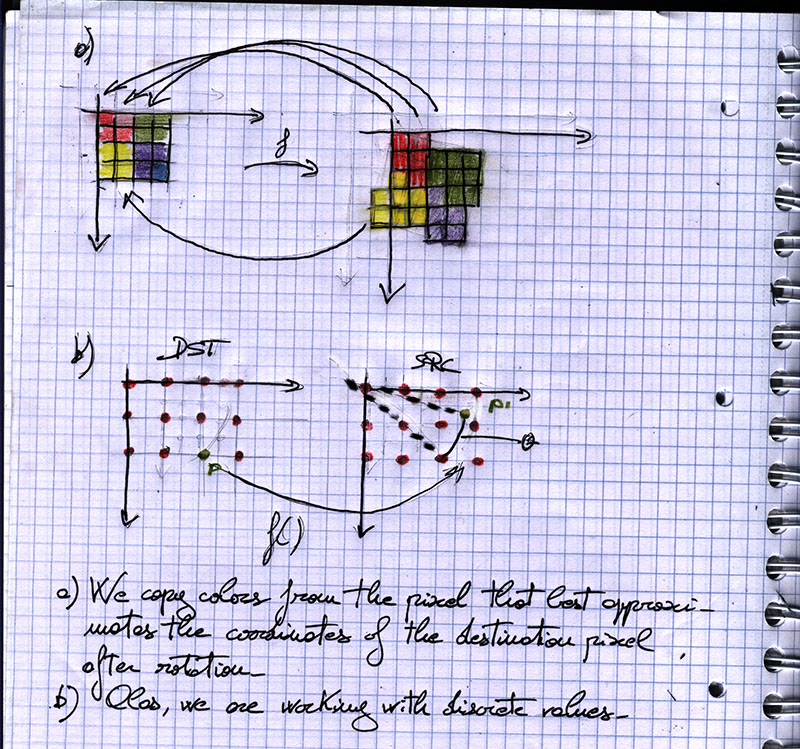This also means that it’s wonderfully more practical to scan the destination, calculate where the destination pixel would end up and copy that instead of the other way around.

Now, all we need to do is to scan the whole of the destination matrix and copy the correct color into each pixel.
A nice for() loop will do.
Here you are.
First in pseudocode:

procedure rotate (angle, src, dst, zoom):
  begin
  invAngle = 2 * PI - angle; // We need to rotate in the opposite direction, remember?
  for (y = 0; y < dstH; y++):
    for (x = 0; x < dstW; x++):
    begin
    targX = ((x * cos(invAngle) - y * sin(invAngle))) * zoom
    targY = ((x * sin(invAngle) + y * cos(invAngle))) * zoom
    dst[x][y] = src[targX][targY]
    end
  end

And now for the actual code used in my patch.
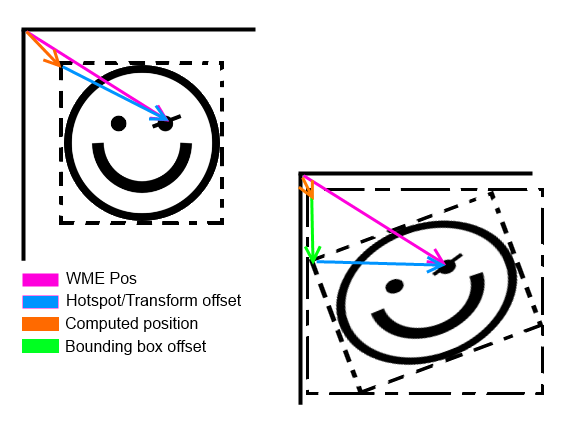
It is only marginally different in that it supports custom centering (omitted above for clarity) and works in degrees instead of radians because that’s what the original Wintermute Engine does.

TransparentSurface *TransparentSurface::rotate(Common::Rect aSrcRect, TransformStruct transform) const {
Point32 newHotspot;
Rect32 rect = TransformTools::newRect(Rect32 (aSrcRect), transform, &newHotspot);
Common::Rect srcRect(0, 0, (int16)(aSrcRect.right - aSrcRect.left), (int16)(aSrcRect.bottom - aSrcRect.top));
Common::Rect dstRect(0, 0, (int16)(rect.right - rect.left), (int16)(rect.bottom - rect.top));
 
TransparentSurface *target = new TransparentSurface();
assert(format.bytesPerPixel == 4);
 
int dstW = dstRect.width();
int dstH = dstRect.height();
 
target->create((uint16)dstW, (uint16)dstH, this->format);
 
uint32 invAngle = (360 - transform._angle) % 360;
float invCos = cos(invAngle * M_PI / 180.0);
float invSin = sin(invAngle * M_PI / 180.0);
 
for (int y = 0; y < dstH; y++) {
for (int x = 0; x < dstW; x++) {
int x1 = x - newHotspot.x;
int y1 = y - newHotspot.y;
 
float targX = ((x1 * invCos - y1 * invSin)) * 100.0 / transform._zoom.x + srcRect.left;
float targY = ((x1 * invSin + y1 * invCos)) * 100.0 / transform._zoom.y + srcRect.top;
 
targX += transform._hotspot.x;
targY += transform._hotspot.y;
 
if (FAST_TRANSFORM) {
nearestCopy(targX, targY, x, y, srcRect, dstRect, this, target);
} else {
bilinearCopy(targX, targY, x, y, srcRect, dstRect, this, target);
}
}
}
return target;
}

…it’s the best thing ever!

We left with me trying to come up with an alternative approach to handle the rotation problem because rotating first and centering later was a mess because of rounding errors piling up.

We also talked about bounding boxes.

So, the good news is that the new approach – it works.

It is definitely better than the other approach, compare:

The old & ugly one is left, the new and pretty one is right.
Even better, you can zoom as much as you want and it will stay perfectly centered instead of wandering around.

It’s actually good enough to play the J.U.L.I.A. Greenlight demo, ladies and gentlemen:

See those rays? Those are rotated & scaled sprites. Yay!
Just wait for the patch to be merged (or for some horribly bad showstopper to pop up), download the demo here and see for yourself.

How did I do it?
Well, we are talking about it in two blog posts:

• Rotation made stupid
• Interpolation made stupid

Now, the only problem with it is that it’s rather slow.
Well, not “with it” (even if the interpolating code could do with some optimization), but with the whole of the GFX/rect subsystem.
Something I’ll tackle on the the second half-term, I guess.

My faithful readers – that is, those who have read my one previous post – will remember how I showed that a surface can be first rotated, then stretched and then correctly positioned by doing a few vector operations..
Well, I was lying.
The thing is, while mathematically the idea is perfectly sound, in practice there is a problem.
Well, two.

Problem one: we’d be doing that with integers.
This means that a. we have single pixel accuracy (which, at best, would mean nearest neighbour) b. we have rounding errors building up.
We need subpixel accuracy for this.

Problem two: I mentioned a magic rotating function that would rotate sprites for me.
Well, we do have one, and it’s called SDL_rotozoom.cpp.
It only has one teensy-weensy problem.
It is not as precise as we’d want when it comes to the bounding box around the rotated sprite.
Basically, what you’d normally expect is this: a different corner of the original sprite ‘pushing’ the edges and causing the resulting sprite to be larger.
Look at this drawing I made for my reference and posted behind my monitor (I can never remember for which range I must use which corner):

This (possibly suboptimal but working) code would give you the exact amount of offset thus produced:

https://github.com/tobiatesan/scummvm/blob/d98529c5aa108488399d41ce7125dc1b421c6a14/engines/wintermute/graphics/transform_tools.cpp

Now, look at this instead:

See that?
Yep.
There is a 1px offset on top and a 2x offset pushing the sprite right.

Those are probably due to rounding errors and various stuff going on in the fixed point calculations done in SDL_rotozoom.cpp (home to the magic function I’ve been talking about till now).
It is exceedingly difficult to compensate for those errors on a case by case basis, to the point that, I realized, the code is practically useless, only good for really low-end devices which benefit from some rather lightweight code.

Could I be completely wrong?

Possibly. I often am.
At the suggestion of my mentor I looked into how the same feature is done in WME:Lite.
Turns out they use SDL to do it – they specify the hotspot and the positioning, and SDL draws “around” the hotspot using fixed point and possibly hardware rendering.

We can’t afford this luxury, though; the code being as it is, we cannot draw “around” the origin.
All pixels for a sprite must be below and right of the origin.

What I’m gonna attempt next will thus be:

1. Calculate the boundaries of the box first and place it firmly where it will end up in the end.
2. In a single pass do an (interpolating?) transform.

This should save me from all the issues above.

Stay tune, more to come.

During the first couple days of GSOC I’ve put some work on the so-called rotozoom functionality – that is, the engine’s ability to take a sprite and stretch/rotate it at will according to game scripts.
As has been said before, this is a key ingredient in at least a couple of games, so it’s the one which will benefit the end user the most.

a. The testbed

For starters, I’ve cooked up a quick test-game for testing purpouses.
It could be mistaken for a Wheel Of Fortune-inspired game, but in truth it’s just a testbed.

I have a pair of sprites that should behave like a protractor if the implementation works correctly.

b. The implementation/1, or: issues for a basic rotozoom implementation:

Now, the rotozoom functionality requires that sprites be
1. Rotated around a custom point, henceforth hotspot
2. Rotated by any number of degrees
3. Stretched at will by any amount, independently on the X and Y-axis.

Assuming that we have a magic function that performs the rotation and returns a rotated sprite (we almost have one, as we’ll see later) what we have here is a problem of offsets.

Three of them.

1. The hotspot/transform offset:

In Wintermute, any Sprite entity’s position is relative to its hotspot.
We’ll call Sprite (with a capital S) the sprite entity in the WME editor and “sprite” a regular sprite.
So, where do we place the “actual sprite”?

We subtract the hotspot coordinates from the position given by WME, so that we obtain the coordinates of the (0,0) point of the sprite with respect to the viewport.

This was a piece of cake, wasn’t it?

It is less cake-y when the image is stretched or rotated, since we must compute the transform for the hotspot location (aka: where the hotspot ends up) and the subtract *that* value.

We use the standard formula for rotation for that:

2. The bounding box offset.
In a sprite we can’t have pixels with negative coordinates.
Thus, when we rotate a sprite, the resulting sprite is taller and wider,  even if the original sprite represented a circular object (because, of course, the transform does not know anything about alpha).
Any point on it can (and most likely) ends up somewhere else in the resulting sprite, even the origin, which may or may not be the same as the hotspot.
Hence, we need to compute the offset to apply to the origin, so that the rotation can appear to “pivot” around the origin (or the hotspot, but we’ll come to it later).

How we compute this offset is the subject of a latter post.

So this is what we do: we subtract these two two vectors from the Pos vector we get from the scripts and are thus able to position the resulting sprite in a way that appears to rotate around the hotspot.

Suppose we want to stretch & rotate the smiley we’ve seen above around its eye.
This is what we do:

Notice the purple vector (origin-eye): it stays the same – the hotspot must stay in the same place.
We subtract the blue vector (the transform for the hotspot) from the purple vector, we subtract the green vector (the bounding box offset) and we get exactly where the resulting sprite must be positioned (the orange vector).

More about the actual implementation w/code snippets soon.

That will be all for today, goodnight!

Hello, dear reader!

I am Tobia, a CompSci student from Italy who has been accepted to work on ScummVM’s WME engine as part of Google Summer of Code 2013.

In case you don’t know ScummVM is an awesome little piece of software that allows you to play, by means of black magick, countless classic adventure games on a wide range of platforms by replicating the functionality of their original engines.

WME is one such engine – instead of being developed in-house for a specific series of games, though, it is a general-purpose piece of software for which a wide range of games has been written, encompassing freeware, commercial and student projects.

Although the games made with WME are hardly classic today, being relatively recent, they could very well be in a couple years.

A port of WME exists (thanks to fellow GSoCer somaen), but it is a bit lacking in certain areas.

My work will consist of filling some gaps, specifically:

• implementing zoom/rotate functionality (which is notably used in a puzzle in J.U.L.I.A.)
• implementing a debugger (which will help development of the engine itself and may make the ScummVM “target” more attractive to WME developers)
• doing some optimization and refactoring, especially with rendering paths
• random bugfixing

Stay tuned for more; during the next few days I expect to get a bit more technical as I start doing some research and try to fix one or two bugs.

Of course, I’ll blog about games when I can, too – games are the whole point, after all, aren’t they?

About me?

Well, I’m a fairly normal guy.

I have a soft spot for black humor, adventure games (guess you didn’t see that coming), reading (all-time favorites: Bulgakov, Hemingway, Vonnegut, Ellison, Ende, Bradbury, Buzzati), obsessing over all sorts of music and doing some jogging when the weather is clear.

Most of all, though, I like doing none of the above, just sitting still on the grass and listening to the birds singing ?