Month: June 2013

My faithful readers – that is, those who have read my one previous post – will remember how I showed that a surface can be first rotated, then stretched and then correctly positioned by doing a few vector operations..
Well, I was lying.
The thing is, while mathematically the idea is perfectly sound, in practice there is a problem.
Well, two.

Problem one: we’d be doing that with integers.
This means that a. we have single pixel accuracy (which, at best, would mean nearest neighbour) b. we have rounding errors building up.
We need subpixel accuracy for this.

Problem two: I mentioned a magic rotating function that would rotate sprites for me.
Well, we do have one, and it’s called SDL_rotozoom.cpp.
It only has one teensy-weensy problem.
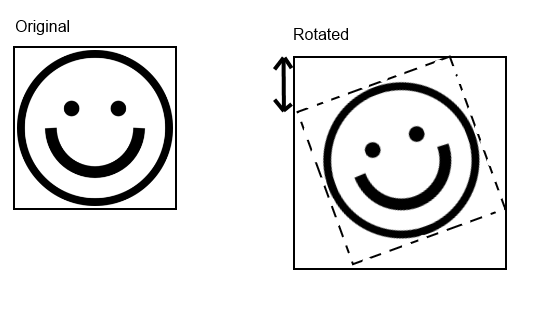
It is not as precise as we’d want when it comes to the bounding box around the rotated sprite.
Basically, what you’d normally expect is this: a different corner of the original sprite ‘pushing’ the edges and causing the resulting sprite to be larger.
Look at this drawing I made for my reference and posted behind my monitor (I can never remember for which range I must use which corner):

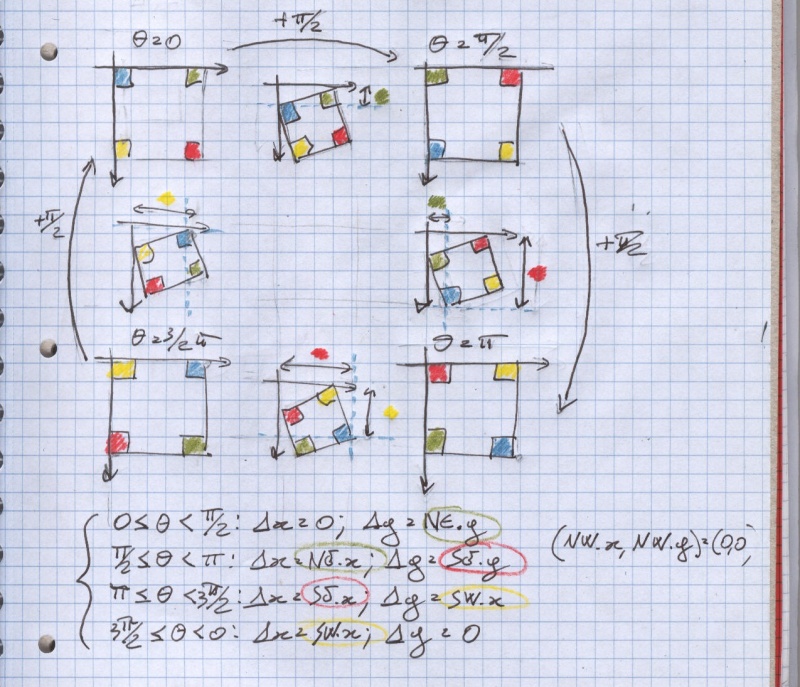This (possibly suboptimal but working) code would give you the exact amount of offset thus produced:

https://github.com/tobiatesan/scummvm/blob/d98529c5aa108488399d41ce7125dc1b421c6a14/engines/wintermute/graphics/transform_tools.cpp

Now, look at this instead:

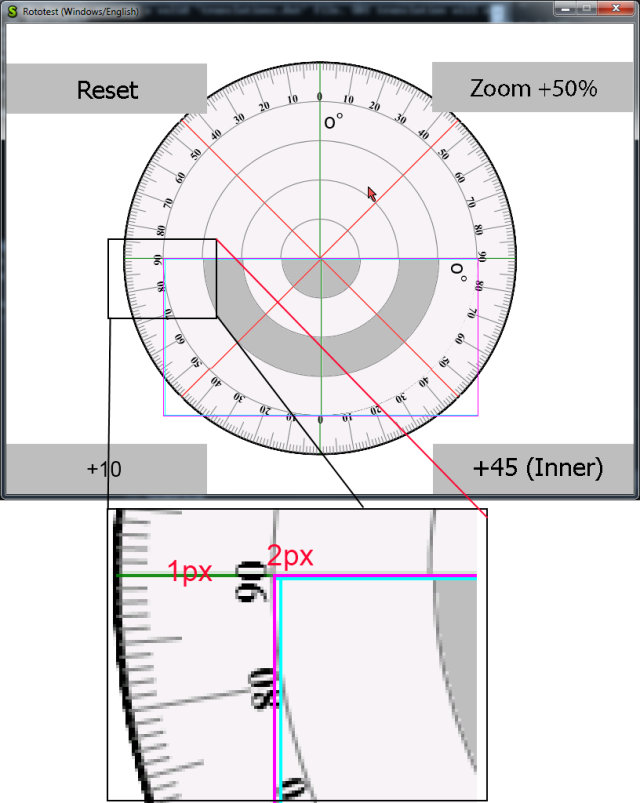See that?
Yep.
There is a 1px offset on top and a 2x offset pushing the sprite right.

Those are probably due to rounding errors and various stuff going on in the fixed point calculations done in SDL_rotozoom.cpp (home to the magic function I’ve been talking about till now).
It is exceedingly difficult to compensate for those errors on a case by case basis, to the point that, I realized, the code is practically useless, only good for really low-end devices which benefit from some rather lightweight code.

Could I be completely wrong?

Possibly. I often am.
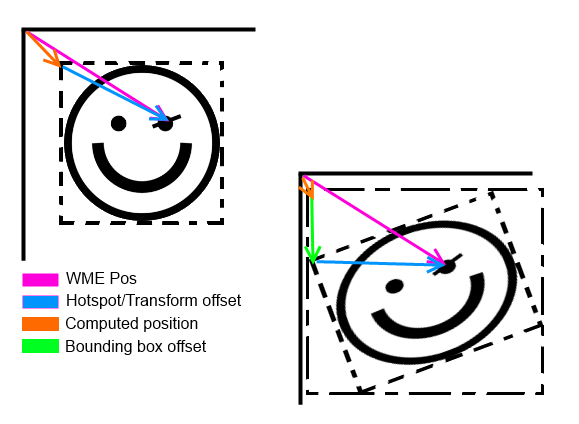
At the suggestion of my mentor I looked into how the same feature is done in WME:Lite.
Turns out they use SDL to do it – they specify the hotspot and the positioning, and SDL draws “around” the hotspot using fixed point and possibly hardware rendering.

We can’t afford this luxury, though; the code being as it is, we cannot draw “around” the origin.
All pixels for a sprite must be below and right of the origin.

What I’m gonna attempt next will thus be:

1. Calculate the boundaries of the box first and place it firmly where it will end up in the end.
2. In a single pass do an (interpolating?) transform.

This should save me from all the issues above.

Stay tune, more to come.

During the first couple days of GSOC I’ve put some work on the so-called rotozoom functionality – that is, the engine’s ability to take a sprite and stretch/rotate it at will according to game scripts.
As has been said before, this is a key ingredient in at least a couple of games, so it’s the one which will benefit the end user the most.

a. The testbed

For starters, I’ve cooked up a quick test-game for testing purpouses.
It could be mistaken for a Wheel Of Fortune-inspired game, but in truth it’s just a testbed.

I have a pair of sprites that should behave like a protractor if the implementation works correctly.

b. The implementation/1, or: issues for a basic rotozoom implementation:

Now, the rotozoom functionality requires that sprites be
1. Rotated around a custom point, henceforth hotspot
2. Rotated by any number of degrees
3. Stretched at will by any amount, independently on the X and Y-axis.

Assuming that we have a magic function that performs the rotation and returns a rotated sprite (we almost have one, as we’ll see later) what we have here is a problem of offsets.

Three of them.

1. The hotspot/transform offset:

In Wintermute, any Sprite entity’s position is relative to its hotspot.
We’ll call Sprite (with a capital S) the sprite entity in the WME editor and “sprite” a regular sprite.
So, where do we place the “actual sprite”?

We subtract the hotspot coordinates from the position given by WME, so that we obtain the coordinates of the (0,0) point of the sprite with respect to the viewport.

This was a piece of cake, wasn’t it?

It is less cake-y when the image is stretched or rotated, since we must compute the transform for the hotspot location (aka: where the hotspot ends up) and the subtract *that* value.

We use the standard formula for rotation for that:

2. The bounding box offset.
In a sprite we can’t have pixels with negative coordinates.
Thus, when we rotate a sprite, the resulting sprite is taller and wider,  even if the original sprite represented a circular object (because, of course, the transform does not know anything about alpha).
Any point on it can (and most likely) ends up somewhere else in the resulting sprite, even the origin, which may or may not be the same as the hotspot.
Hence, we need to compute the offset to apply to the origin, so that the rotation can appear to “pivot” around the origin (or the hotspot, but we’ll come to it later).

How we compute this offset is the subject of a latter post.

So this is what we do: we subtract these two two vectors from the Pos vector we get from the scripts and are thus able to position the resulting sprite in a way that appears to rotate around the hotspot.

Suppose we want to stretch & rotate the smiley we’ve seen above around its eye.
This is what we do:

Notice the purple vector (origin-eye): it stays the same – the hotspot must stay in the same place.
We subtract the blue vector (the transform for the hotspot) from the purple vector, we subtract the green vector (the bounding box offset) and we get exactly where the resulting sprite must be positioned (the orange vector).

More about the actual implementation w/code snippets soon.

That will be all for today, goodnight!