In many of the more relaxed civilizations on the Outer Eastern Rim of the Galaxy, the Hitchhiker’s Guide has already supplanted the great Encyclopaedia Galactica as the standard repository of all knowledge and wisdom, for though it has many omissions and contains much that is apocryphal, or at least wildly inaccurate, it scores over the older, more pedestrian work in two important respects. First, it is slightly cheaper; and second, it has the words “DON’T PANIC” inscribed in large friendly letters on its cover.—Hitchhiker’s Guide to the Galaxy
This is post will go into some detail explaining how to actually rotate a sprite in practice.
It’s a good starting point if you are rolling your own rotozoom function.
It has, naturally, zero academic value and I am also quite sure you can buy manuals that will give you a better idea for just a few dollars.
And you can always troll IRC.
But still.
Now, we assume a little knowledge of linear algebra.
You can probably go ahead all the same if you haven’t taken Algebra 101, but it makes much more sense if you have.
There is countless algebra books which will teach you the basics. Try Strang’s or Nicholson’s.
That said.
Let’s dive in.
Well, a sprite is a matrix of pixels, all right?
To rotate, zoom it and do all the nice things we want to do we need to match a pixel in the source matrix to a pixel in the destination matrix and copy its color.
“This goes here”.
So – look at the source pixel, calculate where it ends up and copy that color. [well, almost, hold on].
Copying a byte is something very simple and your language of choice already offers support for that.
Calculating the destination, well, we need a function for that.
So we have:
(x’, y’) = f(x, y, phi)
don’t we?
There is the textbook formula for rotation:
I’m not giving you a proof or anything (hey, if books aren’t enough you can easily trick a doctoral student into doing the job for you)- it just works.
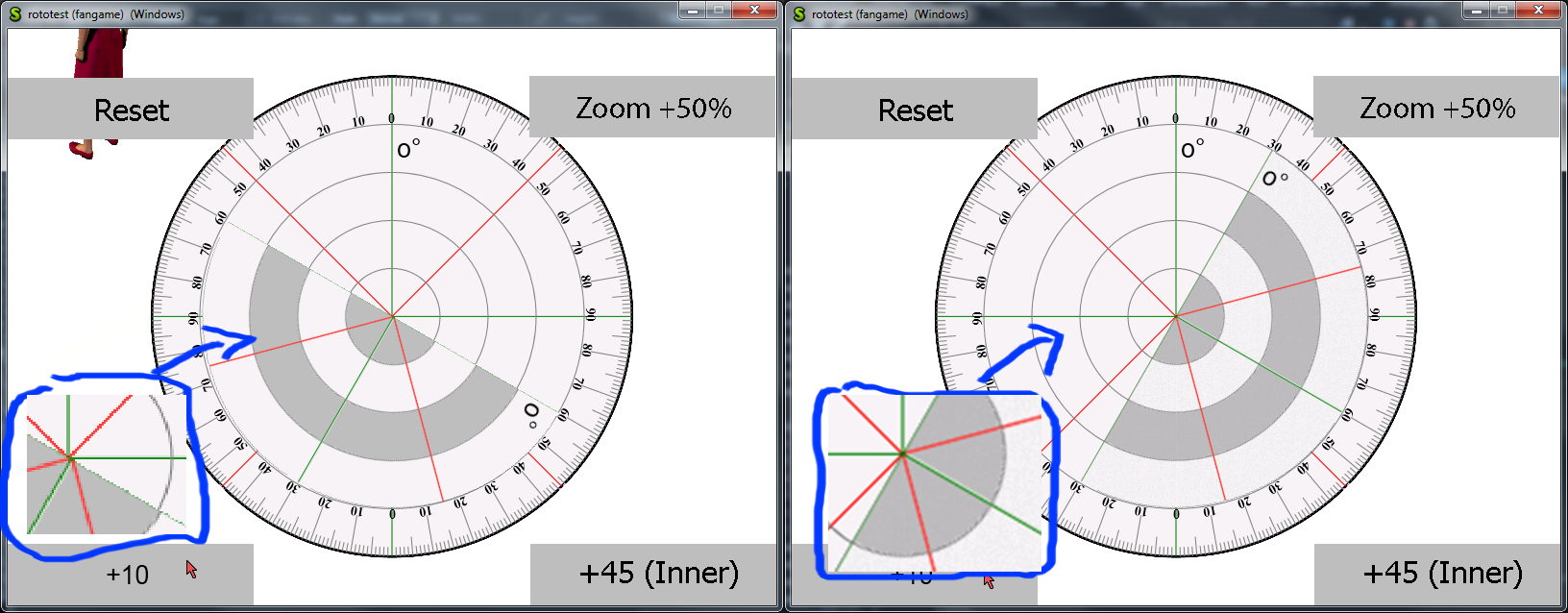
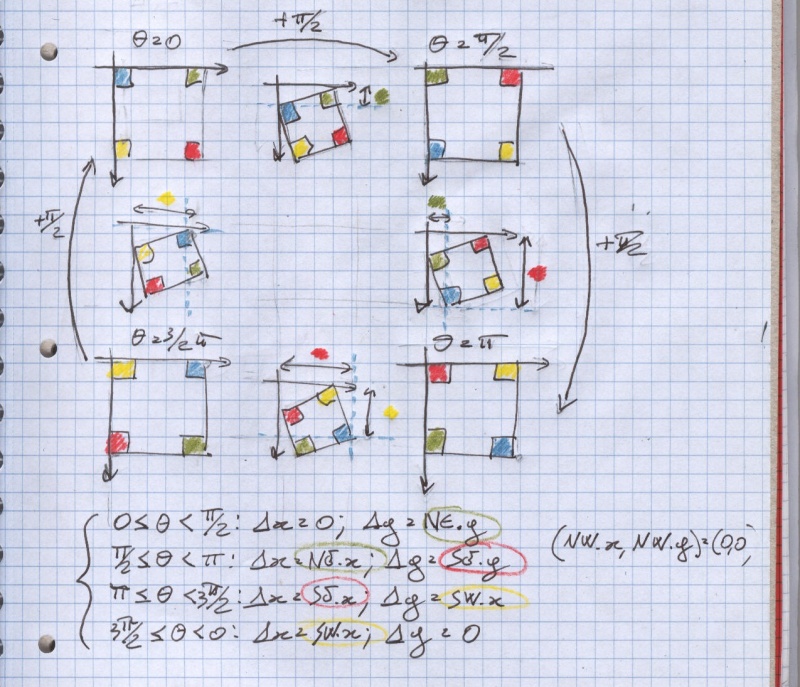
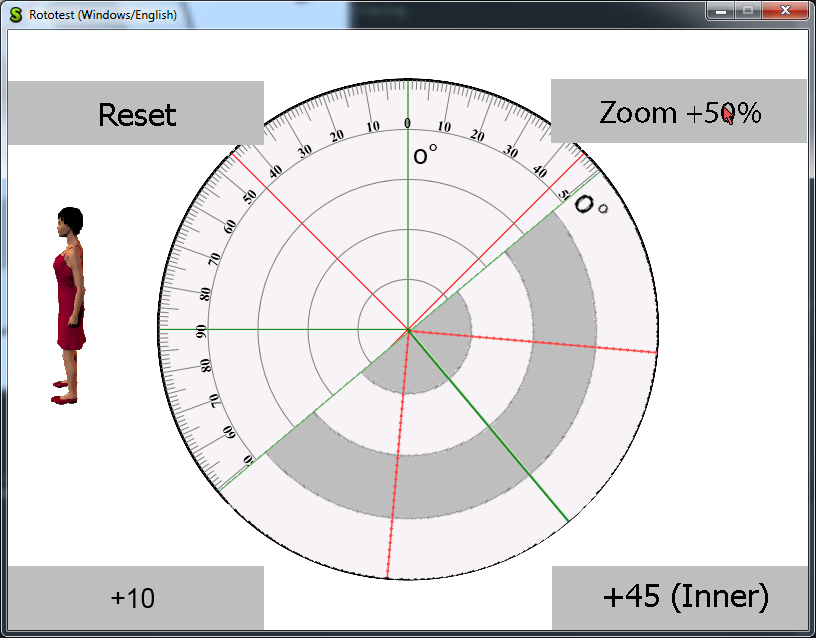
We assume that rotation is carried out around the origin and that no zooming is involved.
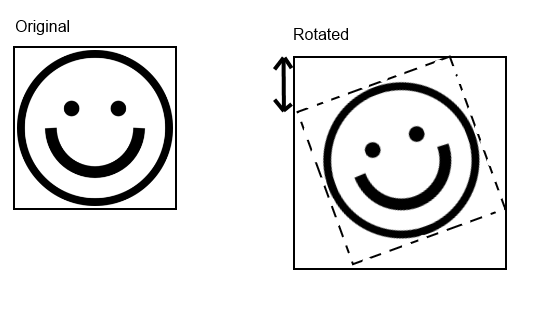
Zooming is actually rather trivial (just multiply by the desidred amount), rotating around a custom point basically means shifting the whole thing so that the hotspot is the new origin, then rotating as above, then shifting again so that the hotspot is where it was in the first place and everything else has moved.
Once you’ve got the simple case, it’s rather simple, though.
See also:
That’s it. Now we can match a point in our destination sprite to a point in our source sprite.
Well, this is not quite it.
You see, while rotating points is a rather mundane matter, we are dealing with pixels, that is… we are working in the discrete.
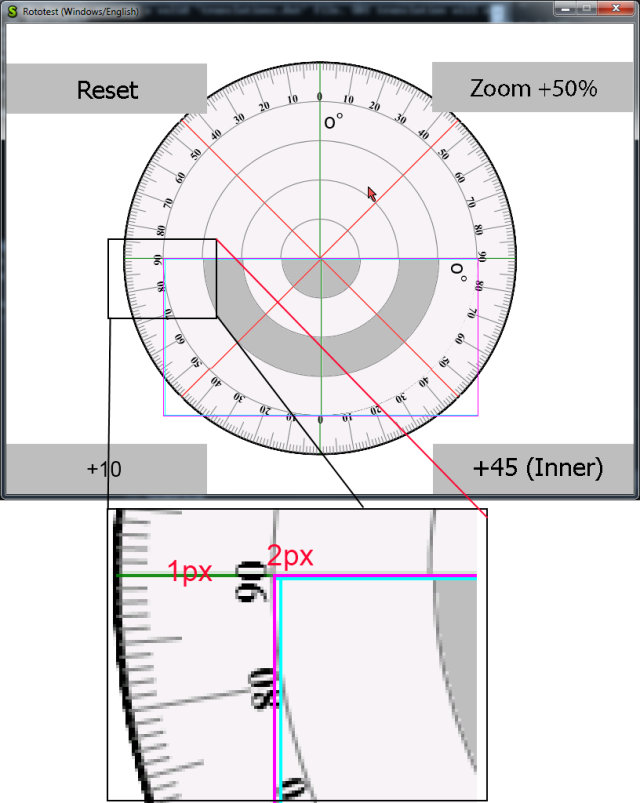
As you can see in the drawing below, P (x,y) in the destination sprite does not match exactly any pixel in the source.
Which means that we must do some approximation.
What do we do? Well, we can either round to the nearest integer or interpolate.
Interpolation will be the subject of the next post, for the moment, we round.
We basically want something like a).
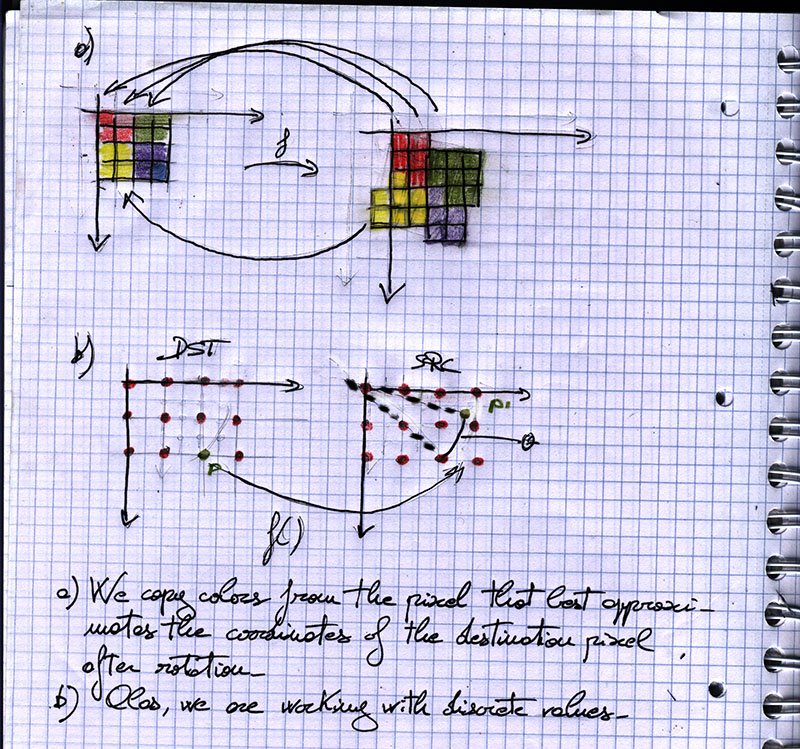 This also means that it’s wonderfully more practical to scan the destination, calculate where the destination pixel would end up and copy that instead of the other way around.
This also means that it’s wonderfully more practical to scan the destination, calculate where the destination pixel would end up and copy that instead of the other way around.
Now, all we need to do is to scan the whole of the destination matrix and copy the correct color into each pixel.
A nice for() loop will do.
Here you are.
First in pseudocode:
procedure rotate (angle, src, dst, zoom):
begin
invAngle = 2 * PI - angle; // We need to rotate in the opposite direction, remember?
for (y = 0; y < dstH; y++):
for (x = 0; x < dstW; x++):
begin
targX = ((x * cos(invAngle) - y * sin(invAngle))) * zoom
targY = ((x * sin(invAngle) + y * cos(invAngle))) * zoom
dst[x][y] = src[targX][targY]
end
end
And now for the actual code used in my patch.
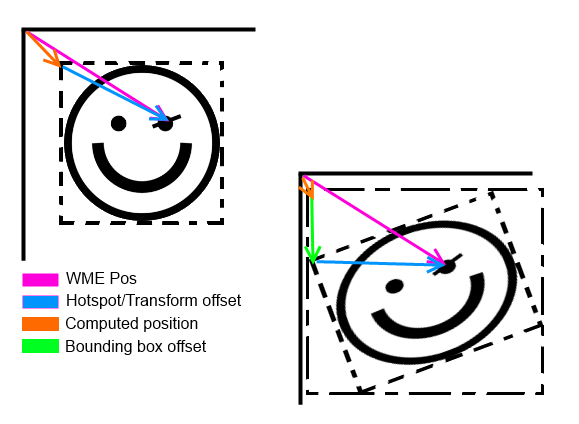
It is only marginally different in that it supports custom centering (omitted above for clarity) and works in degrees instead of radians because that’s what the original Wintermute Engine does.
TransparentSurface *TransparentSurface::rotate(Common::Rect aSrcRect, TransformStruct transform) const {
Point32 newHotspot;
Rect32 rect = TransformTools::newRect(Rect32 (aSrcRect), transform, &newHotspot);
Common::Rect srcRect(0, 0, (int16)(aSrcRect.right - aSrcRect.left), (int16)(aSrcRect.bottom - aSrcRect.top));
Common::Rect dstRect(0, 0, (int16)(rect.right - rect.left), (int16)(rect.bottom - rect.top));
TransparentSurface *target = new TransparentSurface();
assert(format.bytesPerPixel == 4);
int dstW = dstRect.width();
int dstH = dstRect.height();
target->create((uint16)dstW, (uint16)dstH, this->format);
uint32 invAngle = (360 - transform._angle) % 360;
float invCos = cos(invAngle * M_PI / 180.0);
float invSin = sin(invAngle * M_PI / 180.0);
for (int y = 0; y < dstH; y++) {
for (int x = 0; x < dstW; x++) {
int x1 = x - newHotspot.x;
int y1 = y - newHotspot.y;
float targX = ((x1 * invCos - y1 * invSin)) * 100.0 / transform._zoom.x + srcRect.left;
float targY = ((x1 * invSin + y1 * invCos)) * 100.0 / transform._zoom.y + srcRect.top;
targX += transform._hotspot.x;
targY += transform._hotspot.y;
if (FAST_TRANSFORM) {
nearestCopy(targX, targY, x, y, srcRect, dstRect, this, target);
} else {
bilinearCopy(targX, targY, x, y, srcRect, dstRect, this, target);
}
}
}
return target;
}