During the first couple days of GSOC I’ve put some work on the so-called rotozoom functionality – that is, the engine’s ability to take a sprite and stretch/rotate it at will according to game scripts.
As has been said before, this is a key ingredient in at least a couple of games, so it’s the one which will benefit the end user the most.
a. The testbed
For starters, I’ve cooked up a quick test-game for testing purpouses.
It could be mistaken for a Wheel Of Fortune-inspired game, but in truth it’s just a testbed.
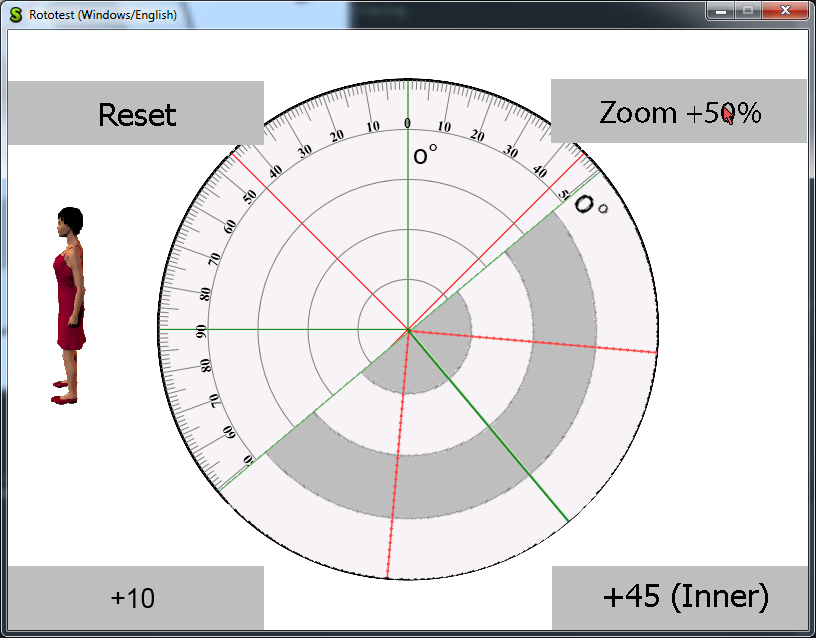I have a pair of sprites that should behave like a protractor if the implementation works correctly.
b. The implementation/1, or: issues for a basic rotozoom implementation:
Now, the rotozoom functionality requires that sprites be
1. Rotated around a custom point, henceforth hotspot
2. Rotated by any number of degrees
3. Stretched at will by any amount, independently on the X and Y-axis.
Assuming that we have a magic function that performs the rotation and returns a rotated sprite (we almost have one, as we’ll see later) what we have here is a problem of offsets.
Three of them.
1. The hotspot/transform offset:
In Wintermute, any Sprite entity’s position is relative to its hotspot.
We’ll call Sprite (with a capital S) the sprite entity in the WME editor and “sprite” a regular sprite.
So, where do we place the “actual sprite”?
We subtract the hotspot coordinates from the position given by WME, so that we obtain the coordinates of the (0,0) point of the sprite with respect to the viewport.
This was a piece of cake, wasn’t it?
It is less cake-y when the image is stretched or rotated, since we must compute the transform for the hotspot location (aka: where the hotspot ends up) and the subtract *that* value.
We use the standard formula for rotation for that:
2. The bounding box offset.
In a sprite we can’t have pixels with negative coordinates.
Thus, when we rotate a sprite, the resulting sprite is taller and wider, even if the original sprite represented a circular object (because, of course, the transform does not know anything about alpha).
Any point on it can (and most likely) ends up somewhere else in the resulting sprite, even the origin, which may or may not be the same as the hotspot.
Hence, we need to compute the offset to apply to the origin, so that the rotation can appear to “pivot” around the origin (or the hotspot, but we’ll come to it later).
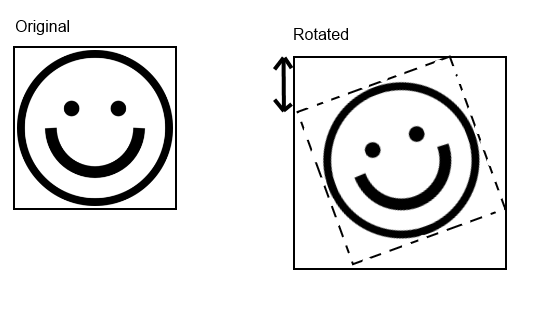How we compute this offset is the subject of a latter post.
So this is what we do: we subtract these two two vectors from the Pos vector we get from the scripts and are thus able to position the resulting sprite in a way that appears to rotate around the hotspot.
Suppose we want to stretch & rotate the smiley we’ve seen above around its eye.
This is what we do:
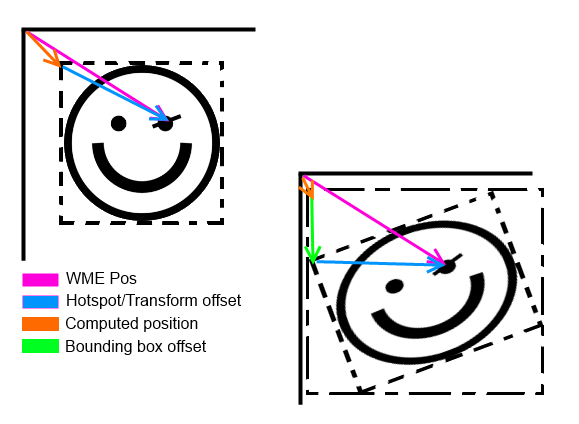Notice the purple vector (origin-eye): it stays the same – the hotspot must stay in the same place.
We subtract the blue vector (the transform for the hotspot) from the purple vector, we subtract the green vector (the bounding box offset) and we get exactly where the resulting sprite must be positioned (the orange vector).
More about the actual implementation w/code snippets soon.
That will be all for today, goodnight!